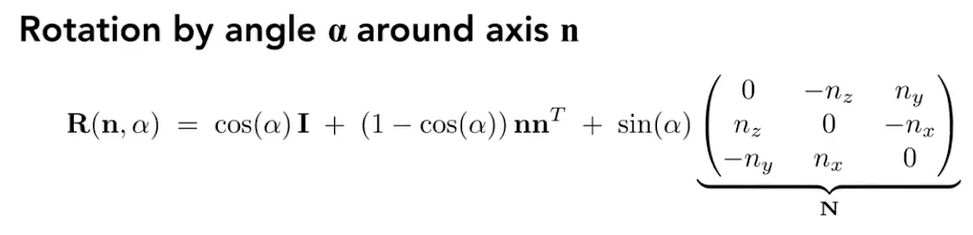[图形]三维变换

2022.01.30修订

3D Transform 三维变换

基本原理和二维变换一致

齐次坐标定义

齐次坐标下的点和向量定义：

• 点：$(x,y,z,1)$
• 向量：$(x,y,z,0)$

一般的，$w\neq 0$的一个点，它也表示三维坐标的点：$(\frac{x}{w},\frac{y}{w},\frac{z}{w})$

更进一步，对齐次坐标下的点乘以任何一个非0的数，它还是表示同一个点

$$(1,0,0,1)=(2,0,0,2)$$

仿射变换

仿射变换使用的齐次坐标下的矩阵：

$$\left( \begin{matrix} x'\\ y'\\ z'\\ 1 \end{matrix} \right)= \left( \begin{matrix} a&b&c&t_x\\ d&e&f&t_y\\ g&h&i&t_z\\ 0&0&0&1 \end{matrix} \right) \left( \begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right)$$

第4行永远是0001，平移还是在第4列，左上角围成的3x3矩阵就是三维空间中的线性变换使用的矩阵

和二维一样，仍然先应用线性变换，再加上平移变换

缩放矩阵

$$\left( \begin{matrix} s_x&0&0&0\\ 0&s_y&0&0\\ 0&0&s_z&0\\ 0&0&0&1 \end{matrix} \right)$$

平移矩阵

$$\left( \begin{matrix} 1&0&0&t_x\\ 0&1&0&t_y\\ 0&0&1&t_z\\ 0&0&0&1 \end{matrix} \right)$$

旋转矩阵

$$\boldsymbol{R}_x= \left( \begin{matrix} 1&0&0&0\\ 0&cos\theta&-sin\theta&0\\ 0&sin\theta&cos\theta&0\\ 0&0&0&1 \end{matrix} \right)$$

$$\boldsymbol{R}_x= \left( \begin{matrix} cos\theta&0&sin\theta&0\\ 0&1&0&0\\ -sin\theta&0&cos\theta&0\\ 0&0&0&1 \end{matrix} \right)$$

$$\boldsymbol{R}_z= \left( \begin{matrix} cos\theta&-sin\theta&0&0\\ sin\theta&cos\theta&0&0\\ 0&0&0&0\\ 0&0&0&1 \end{matrix} \right)$$

稍微复杂一些，三个矩阵都是绕着坐标轴旋转

观察一下可以得知，绕x轴转的时候，x是不变的，所以$\boldsymbol{R}_x$第一行和第一列是1,0,0

绕z轴转的时候一样的

绕y轴旋转的时候，发现它是反过来转的，因为根据右手螺旋定则，$\vec{x}\times\vec{y}$得到$\vec{z}$，那$\vec{x}\times\vec{z}$也可以得到$\vec{y}$

正好和y轴反过来

使用三个简单旋转矩阵可以组合出任意旋转

罗德里格斯旋转公式

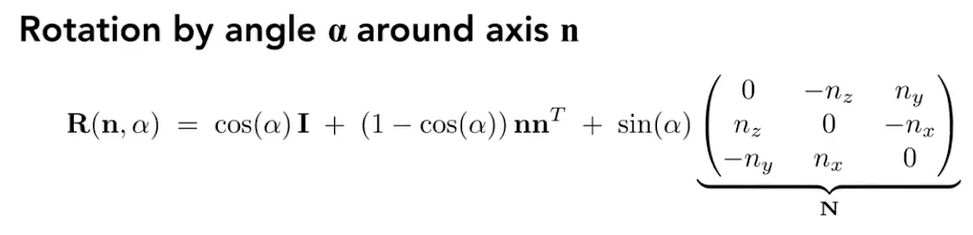
n表示旋转轴（默认旋转轴过原点，n是方向），旋转轴需要起点和方向，这里默认起点在原点上，α表示旋转角

后面大括号的矩阵N，它其实是叉乘

非要绕任意轴转，那就先把它移到原点，再移回去

---

Viewing transformation 观测变换

为了将三维空间中的物体像照相一样变换到二维，我们需要进行观测变换。观测变换包括模型（Model），视图（View），投影（Projection）变换。这一系列变换的矩阵就是MVP矩阵。

View/Camera Transformation 视图变换

找个好角度放摄像机（确定摄像机位置方向）

首先定义个相机

• 位置(Position)$\vec{e}$
• 相机往哪看(LookAt/Gaze Direction)$\vec{g}$
• 向上的方向(Up Direction)$\vec{t}$

拍照的时候，如果周围物体和相机一起做相同的运动，那么拍出来的图也一定不会变化，它们在做相对运动。

既然如此，我们定义：

• 相机永远不动，而且位于坐标原点
• 相机永远往-z方向看
• 相机永远以y轴为向上方向

现在我们要使用矩阵的组合让相机符合定义，也就是：

$$\boldsymbol{M}_{view}=\boldsymbol{R}_{view}\boldsymbol{T}_{view}$$

将摄像机位置$\vec{e}$平移到原点，可以写出平移矩阵T

$$\boldsymbol{T}_{view}= \left( \begin{matrix} 1&0&0&-x_e\\ 0&1&0&-y_e\\ 0&0&1&-z_e\\ 0&0&0&1 \end{matrix} \right)$$

接着将$\vec{g}$旋转到$(0,0,-1)$方向，$\vec{t}$旋转到$(0,1,0)$方向，$\vec{g}\times\vec{t}$旋转到$(1,0,0)$方向

我们可以把这个过程看作：三个向量，同时乘以同一个矩阵，得到三个规范化向量

要将任意的向量旋转到一个规范化向量，不是很好写

但是如果反过来，将规范化的向量旋转到我们需要的方向上，例如把$(0,0,-1)$转到$\vec{g}$方向上，就很好写了

写出来之后再使用逆变换，也就是求它的逆矩阵，就得到了我们需要的$\boldsymbol{R}_{view}$，正好旋转矩阵还是个正交矩阵，逆矩阵等于转置矩阵

所以可以构造一个逆矩阵

$$\boldsymbol{R}_{view}^{-1}= \left( \begin{matrix} a&b&c&0\\ d&e&f&0\\ g&h&i&0\\ 0&0&0&1 \end{matrix} \right)$$

它乘以$(1,0,0,0)$要得到$\vec{g}\times\vec{t}$

$$\left( \begin{matrix} a&b&c&0\\ d&e&f&0\\ g&h&i&0\\ 0&0&0&1 \end{matrix} \right) \left( \begin{matrix} 1\\ 0\\ 0\\ 0 \end{matrix} \right)= \left( \begin{matrix} x_{\vec{g}\times\vec{t}}\\ y_{\vec{g}\times\vec{t}}\\ z_{\vec{g}\times\vec{t}}\\ 0 \end{matrix} \right)$$

很容易解得：

$$\begin{cases} a=x_{\vec{g}\times\vec{t}}\\ d=y_{\vec{g}\times\vec{t}}\\ g=z_{\vec{g}\times\vec{t}} \end{cases}$$

同理，将三组向量分别求出来，最终得到的结果带回矩阵：

$$\boldsymbol{R}_{view}^{-1}= \left( \begin{matrix} x_{\vec{g}\times\vec{t}}&x_{\vec{t}}&x_{-\vec{g}}&0\\ y_{\vec{g}\times\vec{t}}&y_{\vec{t}}&x_{-\vec{g}}&0\\ z_{\vec{g}\times\vec{t}}&z_{\vec{t}}&x_{-\vec{g}}&0\\ 0&0&0&1 \end{matrix} \right)$$

再转置一下：

$$\boldsymbol{R}_{view}=(\boldsymbol{R}_{view}^{-1})^T= \left( \begin{matrix} x_{\vec{g}\times\vec{t}}&y_{\vec{g}\times\vec{t}}&z_{\vec{g}\times\vec{t}}&0\\ x_{\vec{t}}&y_{\vec{t}}&z_{\vec{t}}&0\\ x_{-\vec{g}}&y_{-\vec{g}}&z_{-\vec{g}}&0\\ 0&0&0&1 \end{matrix} \right)$$

其他所有物体要和相机一起做这个变换，保证物体相对位置不变

Projection Transformation 投影变换

投影变换分为正交投影（Orthographic）和透视投影（Perspective）。正交投影中，互相平行的线，投影完后它们还是平行的，而透视投影会逐渐靠近交汇到一起。再简单来说，透视投影近大远小，正交投影是多大就是多大，不会因为摄像机的距离改变。（但是鸽子到底为什么这么大呢.jpg）

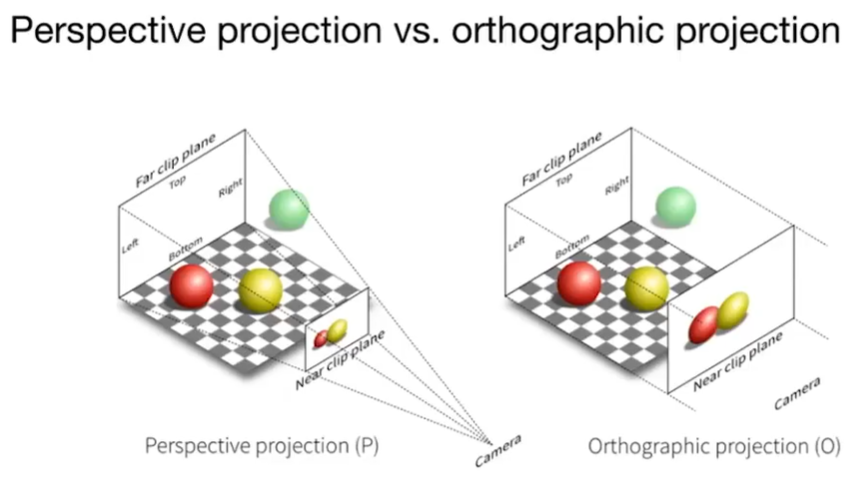
Orthographic Projection 正交投影

1. 把摄像机摆好（原点，看向-Z，向上是Y）
2. 扔掉Z坐标
3. 现在坐标只剩x和y，把坐标按比例缩小到[-1,1]²的矩形内（方便之后的计算）

在空间中划出一块长方体区域，将它映射到一个标准立方体（canonical cube）中

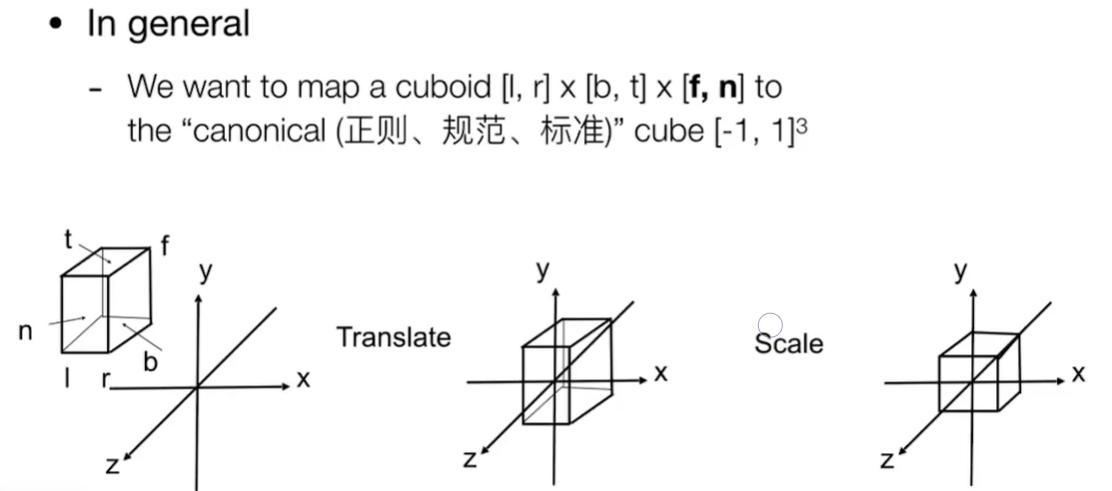
也就是先把长方体中心移动到原点，再将它缩放，很容易将变换写成矩阵形式

$$\boldsymbol{M}_{ortho}= \left( \begin{matrix} \frac{2}{r-l}&0&0&0\\ 0&\frac{2}{t-b}&0&0\\ 0&0&\frac{2}{n-f}&0\\ 0&0&0&1 \end{matrix} \right) \left( \begin{matrix} 1&0&0&-\frac{r+l}{2}\\ 0&1&0&-\frac{t+b}{2}\\ 0&0&1&-\frac{n+f}{2}\\ 0&0&0&1 \end{matrix} \right)$$

需要注意的是，右手坐标系中，划分的长方体区域其实是近大于远（n>f），因为摄像机看向-Z方向，z轴值更大的其实离相机更近

Perspective Projection 透视投影

欧几里得规定，两条永不相交的线是平行线，但是现实的照片中，两条平行线会相交于一个点。在一个平面中（比如同时垂直于两条线的平面），平行线当然是平行的，但它们被投影到另一个平面中时，就不一定了

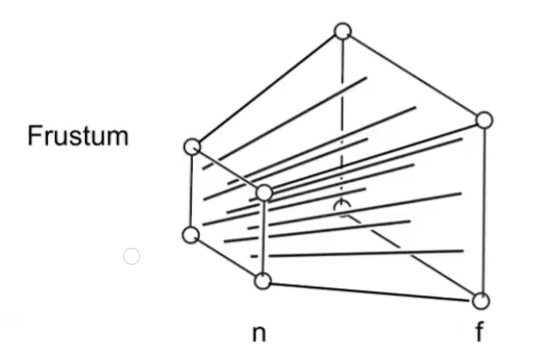
类比正交投影，也要划分一个范围。从一个点延伸出一个四棱锥，定义近的面（n）和远的面（f），n面比f面小

发现它和正交投影的区别仅仅是远的面更大

我们先将透视投影的这个四棱锥给挤压成长方体，再应用正交投影矩阵，问题就解决了

挤压的规则我们规定：

• 近平面（n）上任何一个点永远不变

• 除近平面的面，其他任何点在挤压过程中z轴坐标不变

• 远平面的中心点坐标不变

这样得到的挤压方法就是唯一的

为了挤压四棱锥，我们从四棱锥侧面看它

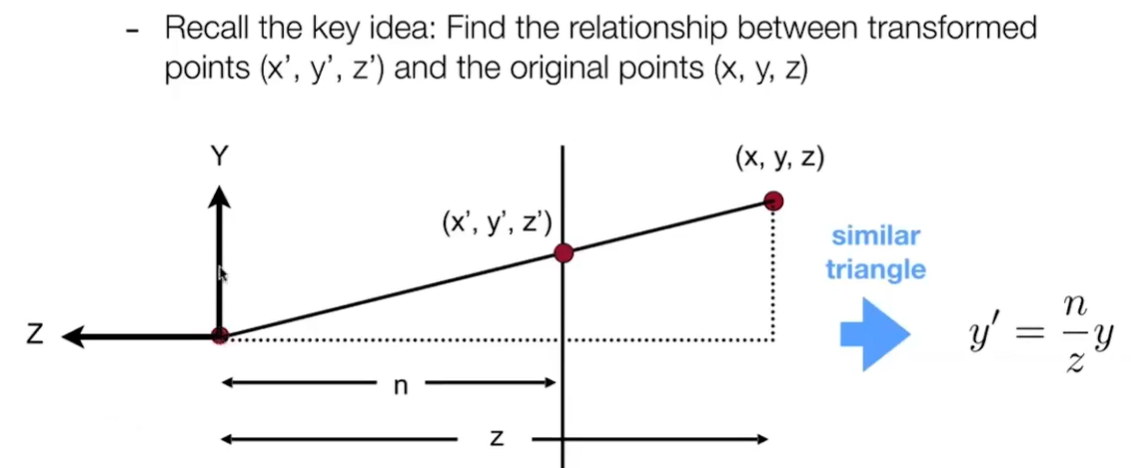
现在有近平面上的点$(x',y',z')$和远平面上的点$(x,y,z)$，根据挤压规则，最后远平面上的点的$y$会和近平面$y'$相等

而且$(x',y',z')$和$(x,y,z)$构成了相似三角形，而$n$和$z$我们都知道

可以使用相似三角形得出$y$与$y'$的关系：

$$\begin{align} \frac{y'}{y}&=\frac{n}{z}\\ y'&=y\frac{n}{z} \end{align}$$

类似的，任意一个平面（在近远平面内且平行于两平面的面）中的点的$y$值都可以通过相似三角形来计算。

而且$x$方向上的挤压也是同一个道理

我们可以得到：

$$\begin{align} x'&=x\frac{n}{z}\\ y'&=y\frac{n}{z} \end{align}$$

齐次坐标下的点坐标变化我们就可以写出来了

$$\left(\begin{matrix} x\\ y\\ z\\ 1 \end{matrix}\right)\rightarrow \left(\begin{matrix} \frac{nx}{z}\\ \frac{ny}{z}\\ unknown\\ 1 \end{matrix}\right)= \left(\begin{matrix} nx\\ ny\\ unknown\\ z \end{matrix}\right)$$

现在我们还不知道z如何变化，所以写成unknown

一个坐标经过矩阵变换，变成了另一个坐标

$$\boldsymbol{M}_{persp\rightarrow ortho} \left(\begin{matrix} x\\ y\\ z\\ 1 \end{matrix}\right)= \left(\begin{matrix} nx\\ ny\\ unknown\\ z \end{matrix}\right)$$

我们可以反推出矩阵的部分元素

$$\boldsymbol{M}_{persp\rightarrow ortho}= \left( \begin{matrix} n&0&0&0\\ 0&n&0&0\\ ?&?&?&?\\ 0&0&1&0 \end{matrix} \right)$$

如何求出第三行呢？这一行和$z$有关

观察四棱锥体，我们发现：

• 任何一个点在近平面上的$z$都不会发生改变
• 任何一个点在远平面上的$z$都不会发生改变

本来近平面上的点的$z$分量全部都是$n$，而且近平面无论如何映射都不会动

利用这一点，我们可以写出近平面的点的映射：

$$\boldsymbol{M}_{persp\rightarrow ortho} \left(\begin{matrix} x\\ y\\ n\\ 1 \end{matrix}\right)= \left(\begin{matrix} x\\ y\\ n\\ 1 \end{matrix}\right)= \left(\begin{matrix} nx\\ ny\\ n^2\\ n \end{matrix}\right)$$

根据映射，可以看看矩阵里的哪些值可以求出来了

$$\left( \begin{matrix} n&0&0&0\\ 0&n&0&0\\ C&D&A&B\\ 0&0&1&0 \end{matrix} \right)\left(\begin{matrix} x\\ y\\ n\\ 1 \end{matrix}\right)= \left(\begin{matrix} nx\\ ny\\ n^2\\ n \end{matrix}\right)$$

可以将第三行单独列出来

$$\left( \begin{matrix} C&D&A&B \end{matrix} \right)\left(\begin{matrix} x\\ y\\ n\\ 1 \end{matrix}\right)=n^2$$

结果中不存在$x$和$y$，所以$C$和$D$直接等于0

$$\left( \begin{matrix} 0&0&A&B \end{matrix} \right)\left(\begin{matrix} x\\ y\\ n\\ 1 \end{matrix}\right)=n^2$$

所以根据近平面上点的特点可以列出方程：

$$nA+B=n^2$$

远平面上点的特点是一样的，我们可以找个特殊点，就是远平面的中心$(0,0,f,1)$，同理可得：

$$fA+B=f^2$$

两方程联立，可以解出

$$\begin{cases} A=n+f\\ B=-nf \end{cases}$$

所以将四棱锥体挤压成长方体的矩阵是：

$$\boldsymbol{M}_{persp\rightarrow ortho}= \left( \begin{matrix} n&0&0&0\\ 0&n&0&0\\ 0&0&n+f&-nf\\ 0&0&1&0 \end{matrix} \right)$$

Questions

Q：挤压四棱锥的时候，近平面和远平面上的点的z值都不变，那锥体里面的点，z值是变大，还是变小，还是不变呢

A：根据矩阵第三行点乘向量，可以列出个式子

$$\frac{z(n+f)-nf}{z}$$

化简一下会发现这是个反比例函数，取$n$到$f$这段，是单调递增的，所以中间这段的z值会被推向远平面

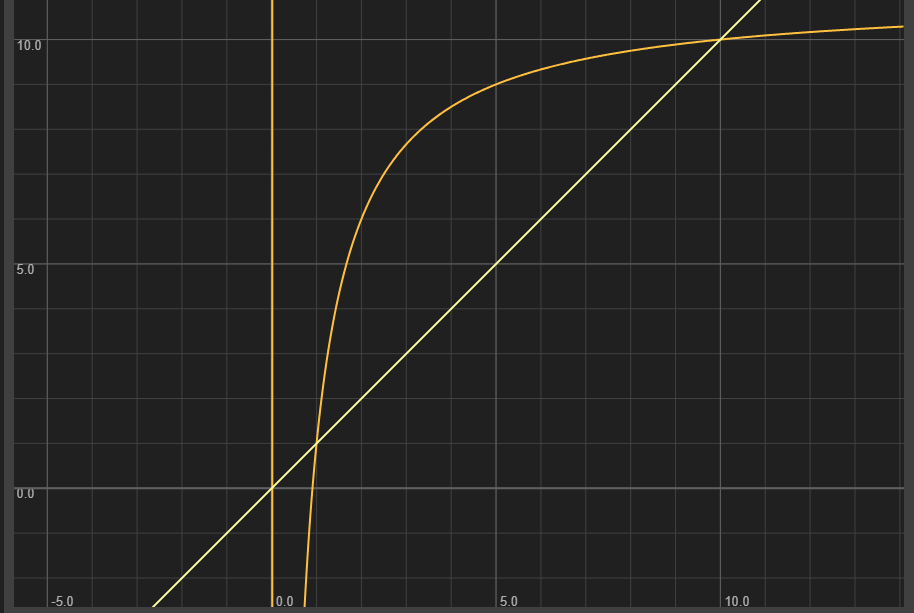
验证一下

假设$n=0.1$，$f=100$，现在有点$(12,15,37)$，挤压后的结果是

$$\boldsymbol{M}_{persp\rightarrow ortho} \left(\begin{matrix} 12\\ 15\\ 37\\ 1 \end{matrix}\right)= \left(\begin{matrix} 1.2\\ 1.5\\ 3693.7\\ 37 \end{matrix}\right)= \left(\begin{matrix} 0.032\\ 0.04\\ 99.8297\\ 1 \end{matrix}\right)$$

确实变大了，也就是说中间的点被推远了

总结一下

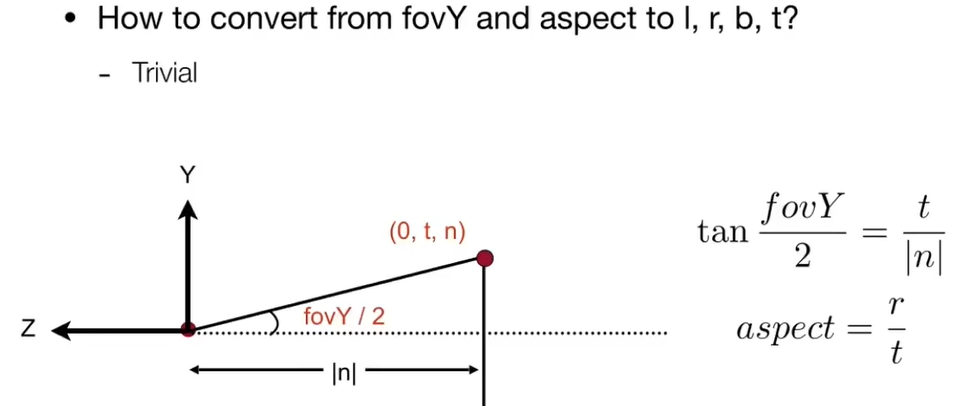
一般来讲，定义透视投影的视锥，先定义near和far。再定义一个宽高比（Aspect ratio）（就是宽除以高）。还会定义视界（field of view,fovY），可视角度比较大就是广角。

怎么算长方体已经很明确了，这里再总结一下把三个矩阵乘在一起的结果

$$\begin{align} \boldsymbol{M}_{persp}&=\boldsymbol{M}_{ortho}\boldsymbol{M}_{persp\rightarrow ortho}\\ &=\left( \begin{matrix} \frac{2}{r-l}&0&0&0\\ 0&\frac{2}{t-b}&0&0\\ 0&0&\frac{2}{n-f}&0\\ 0&0&0&1 \end{matrix} \right) \left( \begin{matrix} 1&0&0&-\frac{r+l}{2}\\ 0&1&0&-\frac{t+b}{2}\\ 0&0&1&-\frac{n+f}{2}\\ 0&0&0&1 \end{matrix} \right)\boldsymbol{M}_{persp\rightarrow ortho}\\ &=\left( \begin{matrix} \frac{2}{r-l}&0&0&-\frac{r+l}{r-l}\\ 0&\frac{2}{t-b}&0&-\frac{t+b}{t-b}\\ 0&0&\frac{2}{n-f}&-\frac{n+f}{n-f}\\ 0&0&0&1 \end{matrix} \right) \left( \begin{matrix} n&0&0&0\\ 0&n&0&0\\ 0&0&n+f&-nf\\ 0&0&1&0 \end{matrix} \right)\\ &=\left( \begin{matrix} \frac{2n}{r-l}&0&-\frac{r+l}{r-l}&0\\ 0&\frac{2n}{t-b}&-\frac{t+b}{t-b}&0\\ 0&0&\frac{n+f}{n-f}&-\frac{2nf}{n-f}\\ 0&0&1&0 \end{matrix} \right) \end{align}$$

再带入

$$\begin{align} t&=ntan\frac{fov}{2}\\ b&=-t\\ r&=t\times aspect\\ l&=-r \end{align}$$

最终的矩阵是：

$$\boldsymbol{M}_{persp}=\left( \begin{matrix} \frac{1}{tan\frac{fov}{2}\times aspect}&0&0&0\\ 0&\frac{1}{tan\frac{fov}{2}}&0&0\\ 0&0&\frac{n+f}{n-f}&-\frac{2nf}{n-f}\\ 0&0&1&0 \end{matrix} \right)$$

顺便求一下视图变换矩阵：

$$\begin{align} \boldsymbol{M}_{view}&=\boldsymbol{R}_{view}\boldsymbol{T}_{view}\\ &= \left( \begin{matrix} x_{\vec{g}\times\vec{t}}&y_{\vec{g}\times\vec{t}}&z_{\vec{g}\times\vec{t}}&0\\ x_{\vec{t}}&y_{\vec{t}}&z_{\vec{t}}&0\\ x_{-\vec{g}}&y_{-\vec{g}}&z_{-\vec{g}}&0\\ 0&0&0&1 \end{matrix} \right) \left( \begin{matrix} 1&0&0&-x_e\\ 0&1&0&-y_e\\ 0&0&1&-z_e\\ 0&0&0&1 \end{matrix} \right)\\ &= \left( \begin{matrix} x_{\vec{g}\times\vec{t}}&y_{\vec{g}\times\vec{t}}&z_{\vec{g}\times\vec{t}}&\boldsymbol{R}_{R1}\cdot\boldsymbol{T}_{C4}\\ x_{\vec{t}}&y_{\vec{t}}&z_{\vec{t}}&\boldsymbol{R}_{R2}\cdot\boldsymbol{T}_{C4}\\ x_{-\vec{g}}&y_{-\vec{g}}&z_{-\vec{g}}&\boldsymbol{R}_{R3}\cdot\boldsymbol{T}_{C4}\\ 0&0&0&1 \end{matrix} \right) \end{align}$$