2022.01.29修订
Linear Transforms 线性变换
Scale 缩放
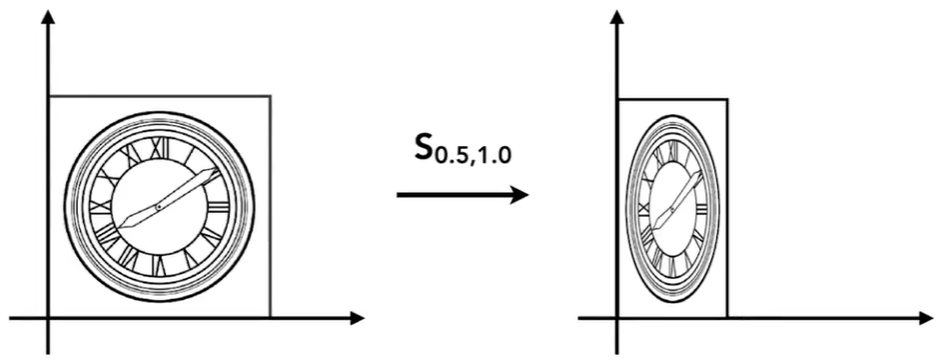
假设图片的原点在世界坐标的原点上,现在我们想把它缩小,写成数学式子很简单:
x′y′=sxx=syy
将它改写为矩阵形式也很简单:
(x′y′)=(sx00sy)(xy)
缩放可以是不均匀的
如果我们把缩放矩阵的元素s设为负值,就可以根据x轴或者y轴镜像反转
Shear 切变
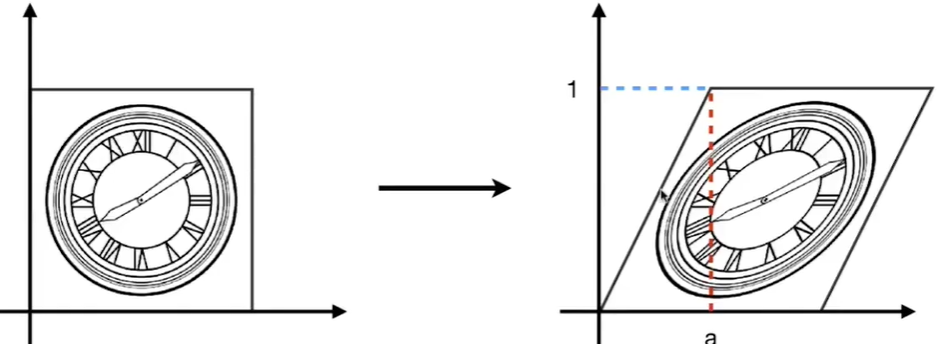
例子中,矩形左上角顶点,经过变换后它的纵坐标不变,横坐标变为a,即(a,1)。又例如矩形左侧边的中点,在变换中向右移动了2a。
也就是说,越靠近顶部,拉得越多,越靠近底部,拉的越少。那么拉动的距离可以写为ay
因此,完整坐标移动可表示为(x+ay,y)。那么,水平方向上的切变,写成矩阵形式就是
(x′y′)=(10a1)(xy)
Rotate 旋转
tips:一般来说,没有其他信息情况下,说旋转都是绕原点,逆时针旋转
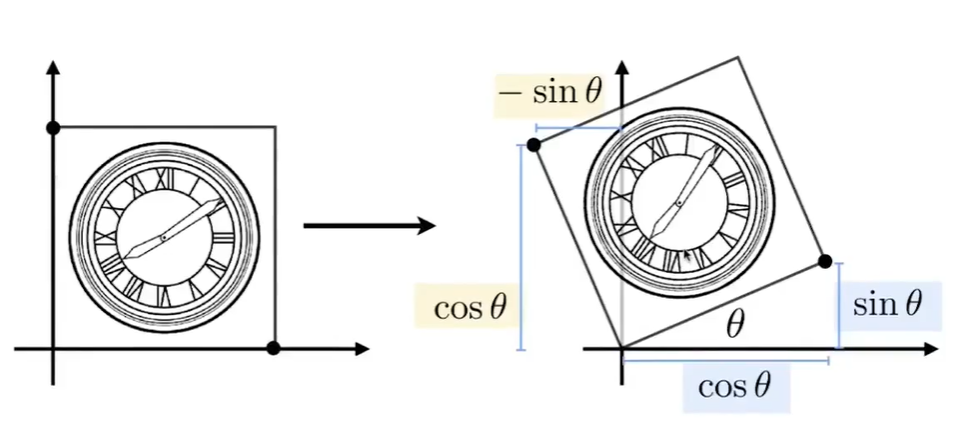
推导矩阵最关键的一点是:找到原坐标(x,y)与结果坐标(x′,y′)之间的对应关系
找到对应关系了,矩阵中的空缺就容易填了
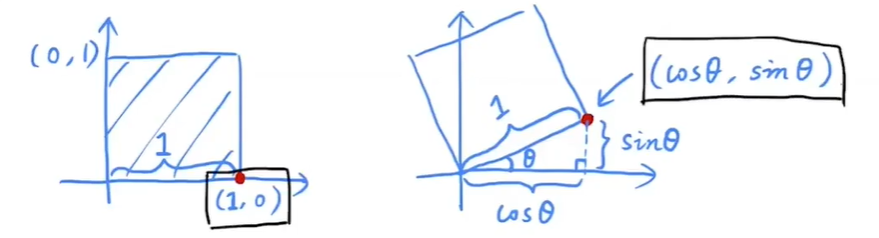
将单位正方体绕原点旋转θ
先看特殊的点(1,0),旋转后的坐标为(x′,y′),往x轴做一条垂线,可以找到一个直角三角形。使用三角函数可以很容易知道该点坐标是(cosθ,sinθ)
那么可以列出等式:
(cosθsinθ)=(ACBD)(10)
再将左侧得矩阵乘法计算一下,可以解得:
{A=cosθC=sinθ
同理,再找一个特殊的点(0,1),它旋转后的点是(−sinθ,cosθ),x轴坐标是−sinθ很容易在图上看出来
再将其带入等式:
(−sinθcosθ)=(cosθsinθBD)(01)
很容易解得
{B=−sinθD=cosθ
(这种方法应该叫待定系数法?)
所以旋转矩阵是:
(cosθsinθ−sinθcosθ)
再推广一下,如果我们想旋转−θ,很简单,把矩阵中的θ都用−θ代替掉就行了
R−θ=(cos(−θ)sin(−θ)−sin(−θ)cos(−θ))=(cosθ−sinθsinθcosθ)
正好等于RθT
而根据定义,旋转θ和−θ正好是一个互逆的操作,也就是
R−θ=Rθ−1
也就得到了:
Rθ−1=RθT
旋转矩阵的逆矩阵等于旋转矩阵的转置,这是个正交矩阵
什么是线性变换
满足
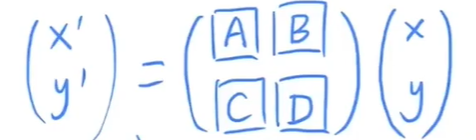
(x′y′)=(ACBD)(xy)
x′=Mx
这种形式的变换,叫做线性变换。(矩阵的维度要和向量相同)
Homogeneous coordinates 齐次坐标
先来看一看平移变换的对应关系
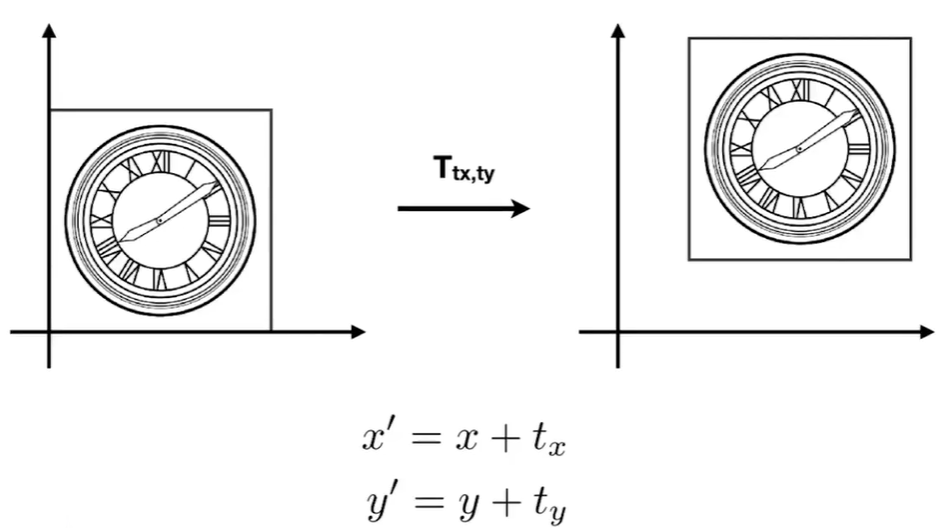
非常简单,但是如果要把这个方程组写成矩阵形式呢?
(x′y′)=(xy)+(txty)
我们没办法把它写成上面线性变换的形式,只能将两个向量相加
让它变得更像线性变换:
(x′y′)=(ACBD)(xy)+(txty)
也就是说,平移不是线性变换
但是数学家并不想让平移变换看作特殊的变换,我们想让这种加法也可以用矩阵乘法来表示。
所以引入了齐次坐标的概念
齐次坐标给点和向量增加一个维度,表示为:
- 点:(x,y,1)
- 向量:(x,y,0)
现在使用齐次坐标的点构造一个矩阵
x′y′w′=100010txty1xy1=x+txy+ty1
正好就是我们需要的平移变换,而且它可以写成矩阵乘以向量的形式了!
但是为什么要将点和向量区别对待?
因为向量具有平移不变性,也就是说,向量不具有平移变换

更深层次的原因是:我们希望向量+向量还是向量,点-点是向量,点+向量还是点。
齐次坐标将点和向量区别对待正好符合向量和点的运算过程
那么点+点是不是没有意义了呢?在齐次坐标中,这种点也有意义:
- 当(x,y,w)是二维的点,也就是w=0,将所有分量都除以w,也就是(wx,wy,1),那它就表示一个点了
这样的点+点形式,在齐次坐标中表示的是两个点的中点坐标
Affine Transformations 仿射变换
将线性变换和平移变换的加法,使用齐次坐标来表示:
x′y′1=ac0bd0txty1xy1
类似这样的变换叫做仿射变换
在表示二维情况下的仿射变换时,齐次坐标的第3行永远是001
Inverse Transform 逆变换
变换后的坐标(x′,y′)如果乘以原矩阵的逆矩阵,就变换回(x,y)了
x=M−1x′
Composite Transform 组合变换

复杂的变换可以通过一系列变换的组合得到
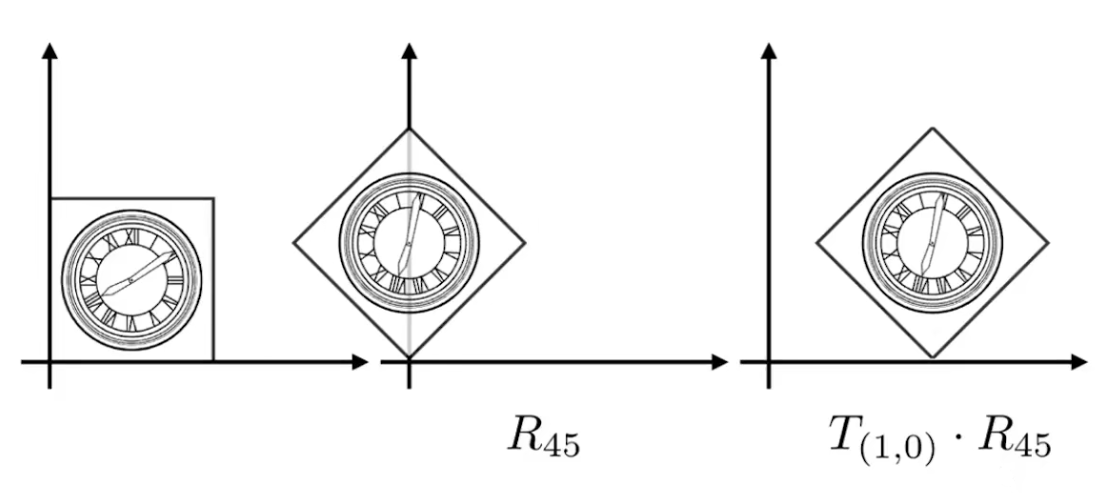
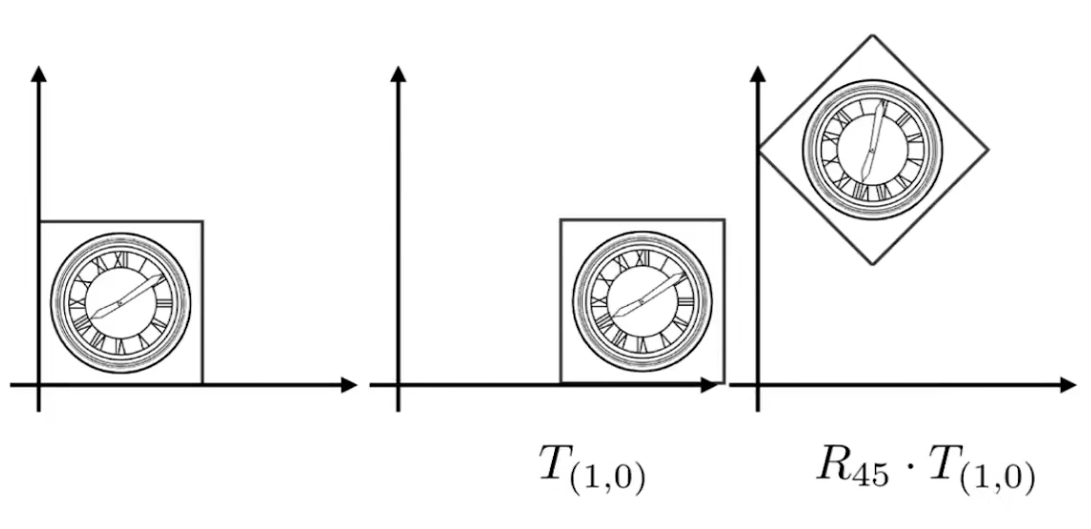
变换的顺序非常重要,我们会发现,旋转和平移的顺序对调,结果会不一样,因为矩阵乘法调换顺序,结果会不一样,因为矩阵乘法不满足交换律
将矩阵应用到点上的时候,由于我们把点看作列向量,所以应用的时候,顺序是从右到左,也就是:
x′=TRx
先乘以R,再乘以T
推广一下,如果有更多的矩阵需要应用到点上,它们的乘积就是:
x′=An(...A2(A1(x)))
回想一下矩阵乘法性质,虽然没有交换律,但是它有结合律,也就是
x′=An(...A2(A1(x)))=(An...A2A1)x
这样,一个矩阵就可以表示之前多个矩阵的变换结果
Questions
Q:既然一个矩阵可以表示这么多变换的结果,而且仿射变换结合了线性变换和平移变换,那到底是先线性变换呢,还是先平移变换呢?
A:观察不使用仿射变换,直接将平移加到线性变换的公式,不难看出,先应用线性变换,再进行平移变换









