Monte Carlo

概率论

$X$：随机变量 (stochastic variables)

$x$：观察$X$的变量(observation of $X$), 或者普通变量

$f(x)$：变量$x$的函数

$p(x)$：随机变量$x$的概率密度, 满足：

$$\int p(x)\mathrm{d}x=1,p(x)\geq 0$$

联合概率密度：

$$p(x,y)=p(x)p(y)$$

条件概率密度：

$$p(y|x)=\frac{p(x,y)}{p(x)}$$

$\hat{I}$：结果$I$的估计器

$E[X]_{X\sim p}$：随机变量的期望, 满足：

$$E[X]_{X\sim p}=\int xp(x)\mathrm{d}x$$

期望有很多性质：

• 线性

$$E[aX+bX]=aE[X]+bE[X]$$

• Law of the unconscious statistician

$$E[f(X)]_{X\sim p}=\int f(x)p(x)\mathrm{d}x$$

• Bernoulli大数定理

$$E[X]=\lim_{N\to\infty}(\frac{1}{N}\sum_{i=0}^N x_i)$$

注意$x_i$独立且同分布(independent and identically distributed)

方差是随机变量与其期望之间的二次偏差的期望(实际上是统计的内容, 不过就放这里吧)：

$$S(X)=E[(X-E[X])^2]=E[X^2]-E[X]^2$$

不相关$X$的线性组合的方差

$$S(\sum^NaX)=a^2\sum^NS(X)$$

Cumulative Distribution Function(CDF)

性质：

• 与pdf关系

$$P(x)=\int_{-\infty}^x p(x)\mathrm{d}x$$

因此pdf是cdf的导数

$$p(x)=\frac{\mathrm{d}P(x)}{\mathrm{d}x}$$

$$\int_a^bp(x)\mathrm{d}x=P(b)-P(a)$$

• 单调递增

• 有界

蒙特卡洛法求解积分

如何直接求解定积分

回顾一下定积分

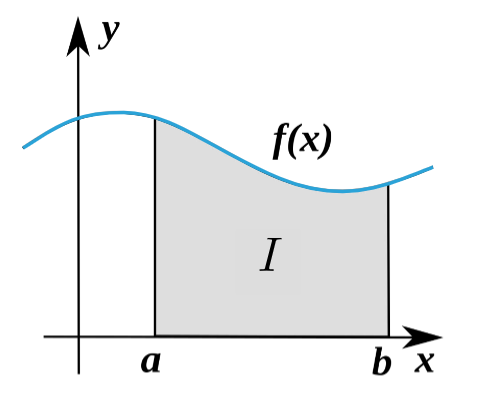
我们有个函数$f(x)$, 我们想在$a$和$b$之间进行数值积分, 换句话数, 我们要计算曲线下的面积$I$, 也就是:

$$I=\int_a^b f(x)\mathrm{d}x$$

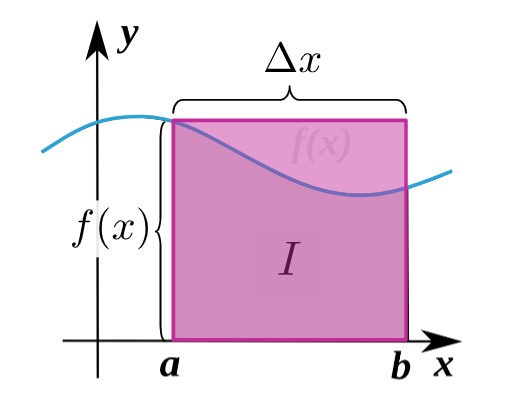
如果把这块区域近似成矩形, 求它的面积非常好求

$$I\approx f(x)\Delta x$$

如果我们细分这块矩形, 它的结果将会更加精确

$$I\approx \sum_{i=0}^N f(x_i)\Delta x$$

细分数量是$N$, 我们很容易得知每一块矩形的长是

$$\Delta x=\frac{b-a}{N}$$

因此, 细分还可以改写成

$$I\approx \frac{b-a}{N}\sum_{i=0}^N f(x_i)$$

如果我们对N取极限, 就是准确的积分结果

$$I=\lim_{N\to\infty}\frac{b-a}{N}\sum_{i=0}^N f(x_i)$$

实际上这就是定积分的标准求解方法

如果我们把函数维度扩展到二维呢?

$$I=\int_D f(x,y)\mathrm{d}x\mathrm{d}y$$

同样的步骤, 分割成小长方体, 计算体积, 细分

最后得到

$$I=\lim_{N\to\infty,M\to\infty}(\frac{D}{NM}\sum_{i=0}^N\sum_{j=0}^M f(x_i,y_j))$$

三维也是一样…扩展到N维, 都是可以工作的

但是, 等等!

由于不知道积分的解析解, 为了计算二维积分, 我们需要在二维上进行抽样, 复杂度是$O(n^2)$, 维度越高复杂度越高, 这几乎是一件不可接受的事情

想想渲染方程, 甚至有好多好多个维度

那如果我们减小精度, 让$\Delta x$更大一些呢?

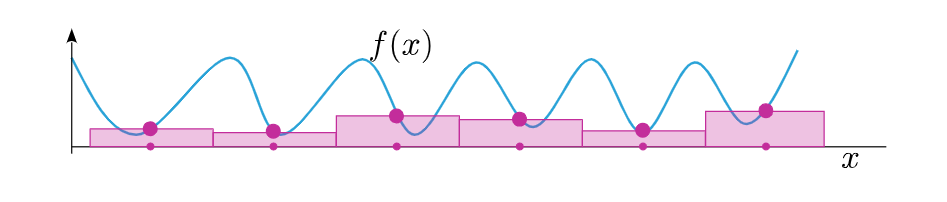
结果明显走样 (aliasing) 了, 计算结果完全错误, 采样频率太低了, (Nyquist frequency描述了准确采样需要的最低频率)

或许我们可以在采样前应用低通滤波器

但有更好的方法, 我们需要一个更好的积分估计器

Monte Carlo 估计器

啥是估计器 (Estimator) ?

总之, 我们先把公式变形一下, 让它看起来更好看一些

$$\begin{align} I&\approx\frac{b-a}{N}\sum_{i=0}^N f(x_i)\\ &=\frac{1}{N}\sum_{i=0}^N(b-a)f(x_i) \end{align}$$

相同的采样数量, 唯一不同的是, 采样点是均匀随机分布在函数上

结果看起来好像有点正确了, 它的结果真的是正确的吗?

回顾一下概率论

我们在$[a,b]$范围内均匀采样, 那么随机变量的概率密度就是

$$p(x)=\frac{1}{b-a}$$

因为

$$\int_a^b p(x)\mathrm{d}x=1$$

把概率密度函数带入积分估计里面

$$\begin{align} I&\approx\frac{1}{N}\sum_{i=0}^N(b-a)f(x_i)\\ &=\frac{1}{N}\sum_{i=0}^N\frac{f(x_i)}{p(x_i)} \end{align}$$

$x_i$服从分布$X\sim p$

回顾一下大数定理

$$E[X]=\lim_{N\to\infty}(\frac{1}{N}\sum_{i=0}^N x_i)$$

大数定理和我们上面计算的式子是不是很像?

$$E[\frac{f(X)}{p(X)}]=\lim_{N\to\infty}(\frac{1}{N}\sum_{i=0}^N\frac{f(x_i)}{p(x_i)})$$

再根据Law of the unconscious statistician

$$E[f(X)]_{X\sim p}=\int f(x)p(x)\mathrm{d}x$$

我们把期望带进去

$$\begin{align} E[\frac{f(X)}{p(X)}]&=\int\frac{f(x)}{p(x)}p(x)\mathrm{d}x \\ &=\int f(x)\mathrm{d}x \\ &=I \end{align}$$

这种方法就是蒙特卡洛法

甚至, $p(x)$可以是任意一种概率分布, 不一定要均匀分布!

等等, 如果$p(x)$是0呢? 虽然在公式里它被约去了

如果$p(x)$是0, 计算结果将会是错误的, 而且计算机除以0会产生NaN…

因此我们需要约定

$$p(x)\gt 0, \forall x \in D$$

最终, 蒙特卡洛估计器的表达式是

$$\hat{I}=\frac{1}{N}\sum_{i=0}^N\frac{f(x_i)}{p(x_i)}$$

Error

通常, 估计器都会有两种错误

• 偏差 (Bias), $E[\hat{I}]\not=I$

• 方差 (Variance)

蒙特卡洛估计器是无偏估计, 它没有偏差

计算一下蒙特卡洛估计器的方差

$$\begin{align} S(\hat{I})&=S(\frac{1}{N}\sum^N\frac{f(X)}{p(X)})\\ &=\frac{1}{N^2}\sum^NS(\frac{f(X)}{p(X)})\\ &=\frac{1}{N^2}NS(\frac{f(X)}{p(X)})\\ &=\frac{1}{N}S(\frac{f(X)}{p(X)}) \end{align}$$

方差与 N 成反比, 而且方差来源只有函数与概率函数的比值

因此蒙特卡洛估计器的偏差会随着采样数量增加而降低

那有没有快速降低方差的方法?

Importance Sampling

我们有个很大的$f(x)$, 但只有个很小很小的$p(x)$, 这意味着f比p的方差非常大

前面说过我们可以自由选择概率密度函数, 因此我们可以选择这个

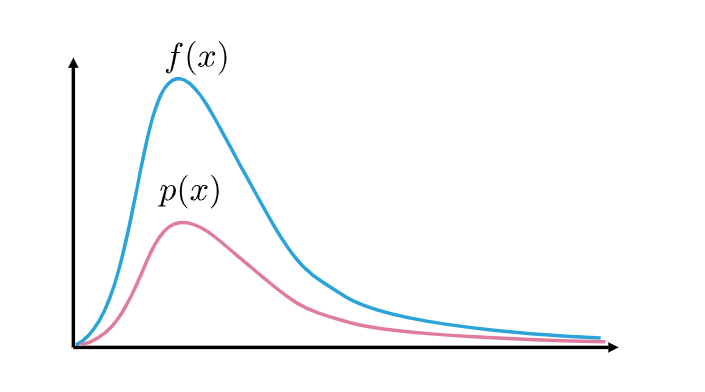
可以看到选一个与$f(x)$几乎成比例的$p(x)$很重要

$$p(x)=sf(x)$$

定义一个常数s来缩放$f(x)$

由于$p(x)$在积分与上积分的值是1

因此

$$s=\frac{1}{\int f(x)\mathrm{d}x}$$

应用这个缩放后

$$S(\frac{f(X)}{p(X)})=S(\frac{f(X)}{sf(X)})=S(\frac{1}{s})=0$$

方差是0! 完美!

但实践中这几乎不可能, 为了得到这样的概率密度, 我们需要的$s$涉及到归一化$f(x)$

如果我们可以归一化$f(x)$, 这意味着我们可以求解定积分, 这样应用蒙特卡洛就没有意义了

但我们还是有办法来逼近这样的概率密度

Inversion Method

假设输入的随机变量$\xi$具有性质:

• 连续

• 均匀分布

• 范围是$[0,1)$

cdf一定是单调递增, 一个随机变量有且只有一个对应的概率, 这意味着cdf一般都具有反函数

这意味着, 给定一个概率, 我们可以用cdf的反函数直接找到它唯一对应的随机变量

$$X_i=P_x^{-1}(\xi)$$

更准确来说, 我们可以通过以下步骤从任意pdf中得到随机样本$X_i$：

• 计算cdf：$P(x)=\int_0^x p(x^{'})\mathrm{d}x^{'}$

• 计算cdf的反函数$P^{-1}(x)$

• 获取一个均匀分布的随机数$\xi$

• 计算$X_i=P^{-1}(\xi)$

例子: 幂分布

给定指数分布的pdf：

$$p(x)=cx^n$$

$c$是规范化pdf的常数, 我们需要先找出pdf的正确表达式

由于pdf积分一定等于1, 而且我们只输入$[0,1)$的值, 因此可以写出：

$$\begin{align} \int_0^1 cx^n\mathrm{d}x&=1\\ c\frac{1}{n+1}x^{n+1}\Big|_{0}^{1}&=1\\ \frac{c}{n+1}&=1\\ c&=n+1 \end{align}$$

因此$p(x)=(n+1)x^n$

现在, 我们可以计算它的cdf了：

$$\begin{align} P(x)&=\int_{0}^{x}p(x)\mathrm{d}x\\ &=\int_{0}^{x}(n+1)x^{n}\mathrm{d}x\\ &=(n+1)\int_{0}^{x}x^n\mathrm{d}x\\ &=x^{n+1}\Big|_{0}^{x}\\ &=x^{n+1} \end{align}$$

它的反函数是：

$$P^{-1}(x)=\sqrt[n+1]{x}$$

因此, 给定一个概率, 我们可以算出它的随机变量

$$X=\sqrt[n+1]{\xi}$$

Inversion Method (2D)

二维的反演方法与一维有许多区别…

如果我们分别对两个pdf应用反演方法, 并输出结果, 结果是错误的

怎么样才能正确得到需要的二维分布?

例子: Unifom Disk

现在我们想在单位圆盘上均匀采样

但是如果我们在圆盘的外接矩形, 也就是单位矩形里均匀采样, 会有一些采样点落到圆盘外

如果使用内接矩形, 这些点又无法完全覆盖圆盘

我们知道除了直角坐标系, 有一种和圆关系密切的坐标系叫做极坐标系

由于是圆盘, 所以我们使用二维极坐标系

定义：

$$r\in[0,1)$$

$$\theta\in[0,2\pi)$$

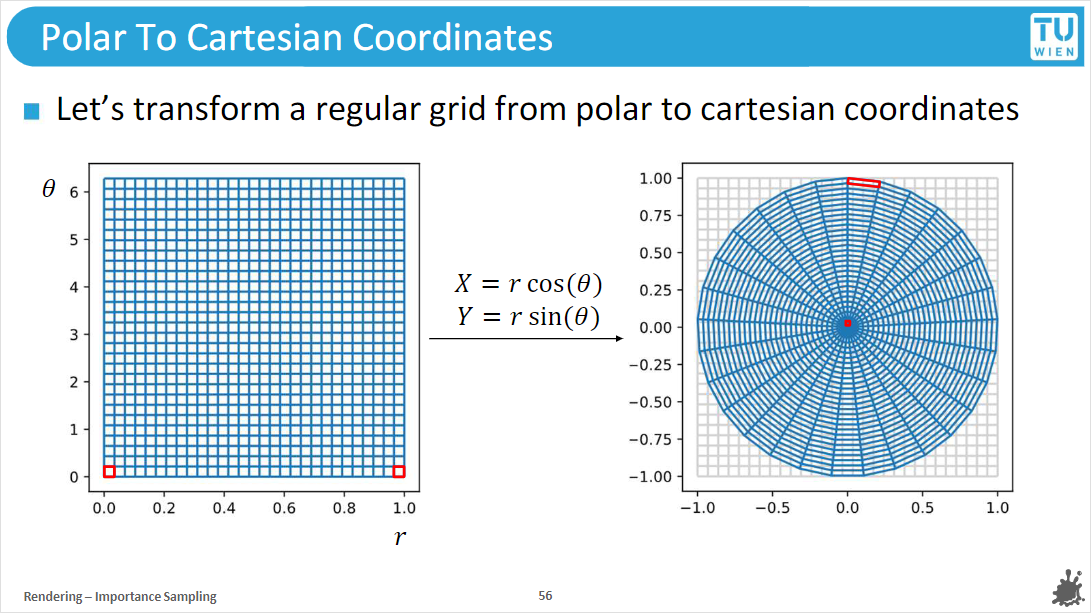
与直角坐标系的转换

$$\left\{ \begin{align} x&=r\mathrm{cos}\theta\\ y&=r\mathrm{sin}\theta \end{align} \right.$$

是不是可以直接拿两个不相关的随机变量$\xi$转换到$r$和$\theta$, 再转换到直角坐标系?

很遗憾, 结果是错的, 为什么?

我们知道圆盘的面积是$\pi r^2$

如果我们把圆盘看作许多个宽为$\Delta r$的同心圆环, 我们的方法实际上就是在所有同心圆环上应用相同数量的采样点

但是同心圆环的周长一直在边长, 那外围能应用的采样点就变少了

也就是说, 分布情况在沿着r的变化而变化

第$j$个圆环的半径等于$r_j=j\Delta r$, 它包含了$(\frac{r_j}{r})^2 N$个采样点

反过来, 第$i$个采样点应该在圆环的位置是：$r_i=r\sqrt{\frac{i}{N}}$

所以实际上$r_i=r\sqrt{\xi_i}$

所以$r$还要开个根号

是的, 这是正确的, 但这样直接针对图像来分析几乎是不可能的, 也不通用

我们需要一种更加通用的推导方法

错误如何发生

我们来分析一下之前我们为什么错了

左边是原始输入的二维随机变量, 右边成比例缩放[0,1]

右边网格最右边的矩形被压缩到原来的二分之一

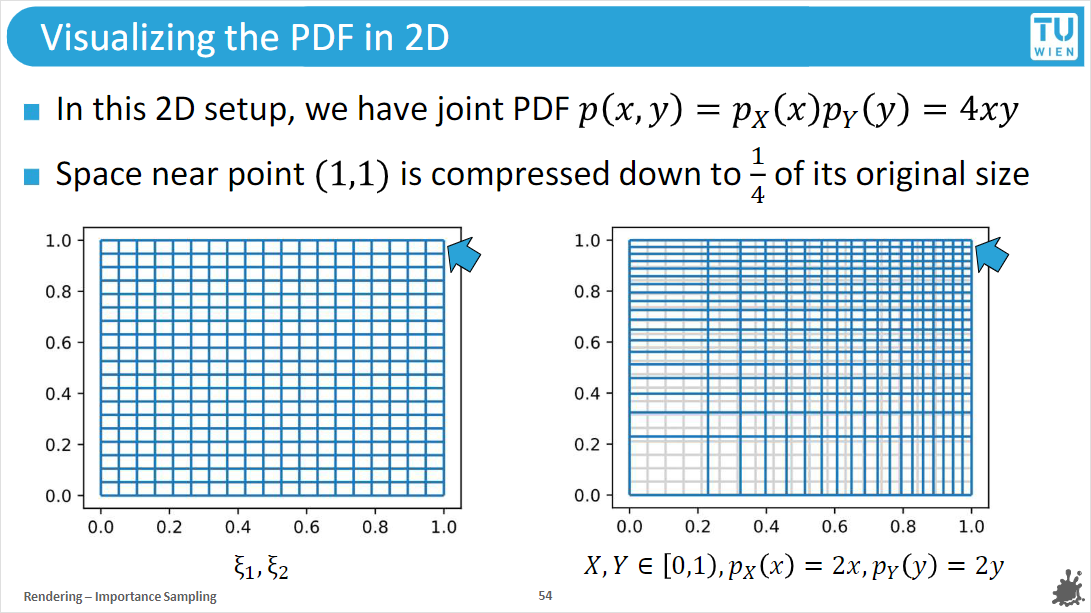
右上角被压缩到原来的四分之一, 左下角放大了四倍

因此, 二维pdf实际上是一个无限小区域面积, 并且在变换pdf时被缩放到另一个区域里

这与我们变换圆盘时发现的现象一致

这种变换改变了我们的样本分布

如果我们知道是什么改变了分布, 我们就可以在蒙特卡洛里加权, 或者在变换后补偿

假设一个随机变量$A$, 它在非线性双射转换(bijective transformation)变换后是$B$, $B=T(A)$

非线性双射变换意味着$b=T(a)$随着$a$单调递增或递减

这意味着每一个$A_i$都对应着唯一的$B_i$, 反之亦然

这种情况下, 两个随机变量的cdf满足$P_B(T(a))=P_A(a)$

如果$b$随着$a$单调递增, 得到:

$$\frac{\mathrm{d}P_B(b)}{\mathrm{d}a}=\frac{\mathrm{d}P_A(a)}{\mathrm{d}a}$$

如果$b$随着$a$单调递减, 得到:

$$-\frac{\mathrm{d}P_B(b)}{\mathrm{d}a}=\frac{\mathrm{d}P_A(a)}{\mathrm{d}a}$$

根据pdf和cdf的性质, 我们知道$p_X$是$P_X$的非负导数

$$\frac{\mathrm{d}P_X(x)}{\mathrm{d}y}=\frac{p_X(x)\mathrm{d}x}{\mathrm{d}y}$$

用这个性质重写单调递增的等式

$$\begin{align} \frac{\mathrm{d}P_B(b)}{\mathrm{d}a}&=\frac{\mathrm{d}P_A(a)}{\mathrm{d}a}\\ \frac{p_B(b)\mathrm{d}b}{\mathrm{d}a}&=\frac{p_A(a)\mathrm{d}a}{\mathrm{d}a}\\ p_B(b)\lvert\frac{\mathrm{d}b}{\mathrm{d}a}\rvert&=p_A(a)\\ p_B(b)&=\lvert\frac{\mathrm{d}b}{\mathrm{d}a}\rvert^{-1}p_A(a) \end{align}$$

当尝试把这个方法应用到单位圆盘，会发现它结果错了，不起作用，因为转换的不仅仅是一个变量的函数，而是两个

我们需要同时考虑到a和b两个变量的变化

解决方法

样本变化

将一组N个的值写为多维变量$\vec{a}$, 将变换后的输出写为$\vec{b}$

$$\vec{a}= \left( \begin{matrix} a_1\\ \vdots\\ a_n \end{matrix} \right) , \vec{b}= \left( \begin{matrix} b_1\\ \vdots\\ b_n \end{matrix} \right)= \left( \begin{matrix} T_1(\vec{a})\\ \vdots\\ T_N(\vec{a}) \end{matrix} \right)= T(\vec{a})$$

必须确保当一个多维变量转化为另一个时，包含联合pdf的全部变化

Jacobian矩阵包含我们可以用向量 a 和 b 形成的所有可能的偏导数的值

$$J_T(\vec{a})= \left( \begin{matrix} \frac{\partial b_1}{\partial a_1} & \cdots & \frac{\partial b_1}{\partial a_N}\\ \vdots & \ddots & \vdots\\ \frac{\partial b_M}{\partial a_1} & \cdots & \frac{\partial b_M}{\partial a_N} \end{matrix} \right)$$

因此，如果我们取第一行和第一列，则该元素表示向量 b 的第一个值如何随向量 a 中的第一个值变化

在第二行第一列中，我们看到向量 b 的第二个值如何随向量 a 中的第一个值变化，以此类推。

这意味着，对于任何给定的位置向量 a，我们可以将雅可比矩阵本身视为一个变换矩阵，它仅对位置向量 a 处的无限小区域有效

最后，Jacobian行列式描述了变换前后面积的变化。因此可以用行列式替换前面的范围变化项

（基本上完全没看懂，先看看怎么应用吧）

看看雅可比矩阵来描述转换到均匀圆盘的变化量

写成向量形式

$$\left( \begin{matrix} x\\ y \end{matrix} \right) =T \left( \begin{matrix} r\\ \theta \end{matrix} \right) = \left( \begin{matrix} r\mathrm{cos}\theta\\ r\mathrm{sin}\theta \end{matrix} \right)$$

计算雅可比行列式

$$\left| \begin{matrix} \frac{ \partial T \left( \begin{matrix} r\\ \theta \end{matrix} \right) }{\partial \left( \begin{matrix} r\\ \theta \end{matrix} \right) } \end{matrix} \right| = \left| J_T\right| = \left| \left( \begin{matrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial\theta}\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial\theta} \end{matrix} \right) \right| = \left| \left( \begin{matrix} \mathrm{cos}\theta & -r\mathrm{sin}\theta\\ \mathrm{sin}\theta & r\mathrm{cos}\theta \end{matrix} \right) \right| =r$$

替换掉变化量, 可以得到

$$p(x,y)=\frac{1}{r}p(r,\theta)$$

它告诉我们，直角坐标系中的均匀概率密度与极坐标系中的r成正比

正确采样联合概率密度函数

要正确转换二维分布，最后一个问题是正确采样联合概率密度函数

到目前为止，我们只讨论了不相关变量的转换

在有两个随机变量的情况下，给定它们的联合 PDF，我们可以这样做：我们首先计算一个变量的边缘密度函数，然后计算另一个变量的条件密度函数

我们将使用这些边际和条件密度函数，而不是单个变量的 PDF，因为只有在它们独立时才能保证有效

但是我们需要对它们执行的步骤是和之前一样的：对它们求积分，对不定积分求逆，并将它们用于采样

换句话说，我们要做的是：首先对一个随机变量进行抽样，然后对另一个进行抽样，因为第二个变量的抽样可能取决于第一个变量返回的结果

边缘概率密度是啥？举个例子，如果在 x 和 y 的所有可能组合中，我们有 50% 的机会看到 x=1，那么对于 x = 1，基于 p(x,y) 的 x 的边际密度将为 0.5

首先联合pdf的随机变量$X$和$Y$有范围$[a_X,b_X)$和$[a_Y,b_Y)$

将$p_X(x)$看作$p(x,y)$在$x$点时，$y$可能取值的平均密度

我们可以通过整合所有其他函数来获得其中一个的边际密度函数，例如

$$p_X(x)=\int_{a_Y}^{b_Y}p(x,y)\mathrm{d}y$$

接着，相对于x，y的条件概率密度是

$$p(y|x)=\frac{p(x,y)}{p_X(x)}$$

例子：Unifom Disk 正式解决方案

再来一遍，这次我们用最好的方法来推导分布变换

我们知道采样域的总面积为$\pi$，并且我们知道pdf必须在采样域上积分为1，因此我们知道任何一个点的联合概率密度应该是$\frac{1}{pi}$

$$p(x,y)=\frac{1}{\pi}$$

从之前计算的jacobian行列式我们知道了，分布转换时会有个大小为r的系数

$$p(r,\theta)=rp(x,y)$$

因此，我们希望

$$p(r,\theta)=\frac{r}{\pi}$$

最后，我们计算r的边缘概率密度

$$\begin{align} p_R(r)&=\int_{0}^{2\pi}p(r,\theta)\mathrm{d}\theta\\ &=\int_{0}^{2\pi}\frac{r}{\pi}\mathrm{d}\theta\\ &=\frac{r}{\pi}\int_{0}^{2\pi}\mathrm{d}\theta\\ &=\frac{r}{\pi}(2\pi-0)\\ &=2r \end{align}$$

在r条件下，$\theta$的条件概率密度是

$$p(\theta|r)=\frac{p(r,\theta)}{p_R(r)}=\frac{1}{2\pi}$$

对边缘概率密度和条件概率密度分别应用Inversion Method

$$r\in[0,1]$$

因此积分上下限是0到1

$$\begin{align} P(r)&=\int_{0}^{1}p_R(r)\mathrm{d}r\\ &=\int_{0}^{1}2r\mathrm{d}r\\ &=r^2 \end{align}$$

反函数

$$P^{-1}(r)=\sqrt{r}$$

同理，$\theta$的定义域是

$$\theta\in[0,2\pi]$$

对条件概率密度积分

$$\begin{align} P(\theta)&=\int_{0}^{2\pi}p(\theta|r)\mathrm{d}\theta\\ &=\int_{0}^{2\pi}\frac{1}{2\pi}\mathrm{d}\theta\\ &=\frac{1}{2\pi}(2\pi-0)\\ &=1 \end{align}$$

它是常数函数，这意味着直接转换分布也不会有问题

结论：

$$\left\{ \begin{align} r&=P_R^{-1}(\xi_1)=\sqrt{\xi_1}\\ \theta&=P_{\Theta}^{-1}(\xi_2)=2\pi\xi_2 \end{align} \right.$$

例子：Unifom Hemisphere

假设所有点都落在半球表面，也就是球半径为1

$$\sqrt{x^2+y^2+z^2}=1$$

定义域

$$\theta\in[0,\frac{2}{\pi}), \phi\in[0,2\pi)$$

球面坐标系与直角坐标系转换：

$$\left\{ \begin{align} x&=r\mathrm{sin}\theta\mathrm{cos}\phi\\ y&=r\mathrm{sin}\theta\mathrm{sin}\phi\\ z&=r\mathrm{cos}\theta \end{align} \right.$$

雅可比行列式：

$$\begin{align} \left| \left( \begin{matrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial\theta} & \frac{\partial x}{\partial\phi}\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial\theta} & \frac{\partial y}{\partial\phi}\\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial\theta} & \frac{\partial z}{\partial\phi} \end{matrix} \right) \right| &= \left| \left( \begin{matrix} \mathrm{sin}\theta\mathrm{cos}\phi & r\mathrm{cos}\theta\mathrm{cos}\phi & -r\mathrm{sin}\theta\mathrm{sin}\phi\\\ \mathrm{sin}\theta\mathrm{sin}\phi & r\mathrm{cos}\theta\mathrm{sin}\phi & r\mathrm{sin}\theta\mathrm{cos}\phi\\ \mathrm{cos}\theta & -r\mathrm{sin}\theta & 0 \end{matrix} \right) \right| \\&= r^{2}\mathrm{sin}\theta\mathrm{cos}^2\theta\mathrm{cos}^2\phi+r^{2}\mathrm{sin}^{3}\theta\mathrm{sin}^{2}\phi+ r^{2}\mathrm{sin}\theta\mathrm{cos}^2\theta\mathrm{sin}^2\phi+r^{2}\mathrm{sin}^{3}\theta\mathrm{cos}^{2}\phi\\ &=r^{2}\mathrm{sin}\theta(\mathrm{cos}^2\theta\mathrm{cos}^2\phi+\mathrm{sin}^2\theta\mathrm{sin}^2\phi+ \mathrm{cos}^2\theta\mathrm{sin}^2\phi+\mathrm{sin}^2\theta\mathrm{cos}^2\phi)\\ &=r^{2}\mathrm{sin}\theta(\mathrm{sin}^{2}\theta(\mathrm{sin}^{2}\phi+\mathrm{cos}^{2}\phi)+\mathrm{cos}^{2}\theta(\mathrm{sin}^{2}\phi+\mathrm{cos}^{2}\phi))\\ &=r^{2}\mathrm{sin}\theta(\mathrm{sin}^{2}\theta+\mathrm{cos}^{2}\theta)\\ &=r^{2}\mathrm{sin}\theta \end{align}$$

因此，在球坐标系下，联合概率密度是

$$p(r,\theta,\phi)=\frac{r^{2}\mathrm{sin}\theta}{2\pi}$$

因为我们假设是单位半球，因此$r$永远为1

计算$\theta$边缘概率密度

$$\begin{align} p_\Theta(\theta)&=\int_{0}^{2\pi}\frac{\mathrm{sin}\theta}{2\pi}\mathrm{d}\phi\\ &=\frac{\mathrm{sin}\theta}{2\pi}(\int_{0}^{2\pi}\mathrm{d}\phi)\\ &=\mathrm{sin}\theta \end{align}$$

计算$\theta$的cdf

$$\begin{align} P_\Theta(\theta)&=\int_{-\infty}^{\theta}\mathrm{sin}\theta\mathrm{d}\theta\\ &=\int_{0}^{\theta}\mathrm{sin}\theta\mathrm{d}\theta\\ &=-\mathrm{cos}\theta\Big|_{0}^{\theta}\\ &=1-\mathrm{cos}\theta \end{align}$$

计算$\theta$的cdf的反函数

$$P_\Theta^{-1}(\theta)=\mathrm{cos}^{-1}(1-\xi)$$

因为$\xi\in[0,1)$，所以可以用$\xi$替换掉$1-\xi$

计算对于$\theta$来说，$\phi$的条件概率密度是

$$\begin{align} p_\Phi(\phi|\theta)&=\frac{p(\theta,\phi)}{p_\Theta(\theta)}\\ &=\frac{1}{2\pi} \end{align}$$

计算$\phi$的cdf

$$\begin{align} P_\Phi(\phi)&=\int_{0}^{\phi}\frac{1}{2\pi}\mathrm{d}\phi\\ &=\frac{\phi}{2\pi} \end{align}$$

计算$\phi$的cdf的反函数

$$P_\Phi^{-1}(\phi)=2\pi\xi$$

因此概率分布转换是

$$\left\{ \begin{align} \theta&=\mathrm{cos}^{-1}\xi_{1}\\ \phi&=2\pi\xi_{2} \end{align} \right.$$

又因为

$$\mathrm{cos}\theta=\xi_1$$

而且众所周知，

$$\mathrm{sin}^{2}\theta+\mathrm{cos}^{2}\theta=1$$

所以

$$\begin{align} \mathrm{sin}\theta&=\sqrt{1-\mathrm{cos}^2\theta}\\ &=\sqrt{1-\xi_1^2} \end{align}$$

带入直角坐标系转球面坐标系

$$\left\{ \begin{align} x&=\sqrt{1-\xi_1^2}\mathrm{cos}(2\pi\xi_2)\\ y&=\sqrt{1-\xi_1^2}\mathrm{sin}(2\pi\xi_2)\\ z&=\xi_1 \end{align} \right.$$

例子：Diffuse BRDF

首先，让我们再再再回顾一下渲染方程里的反射部分

$$\int_\Omega f_r(x,\omega\to v)L(x\gets\omega)\mathrm{cos}\theta_\omega\mathrm{d}\omega$$

假设现在BRDF是Lambertian，它实际上是个常数$\frac{R}{\pi}$

cosine项也是可知的，它取决于$\omega$

最麻烦的部分是光照部分$L(x\gets\omega)$，我们不知道间接光会从哪里来，这个参数甚至还是递归的

我们完全不知道有关$L$的信息，那就只能假设光线会从四面八方均匀射入，令它等于常数$k$

$$\int_\Omega \frac{R}{\pi}k\mathrm{cos}\theta_\omega\mathrm{d}\omega$$

这样，被积函数的形状仅取决于$\mathrm{cos}\theta_\omega$，给定pdf：

$$p(\omega)=c\mathrm{cos}\theta$$

首先计算pdf，由于采样点只会落到半球上，因此整个半球上的cdf是1

$$\int_\Omega p(\omega)\mathrm{d}\omega=1$$

众所周知，任意球面的微分面积是

$$\mathrm{d}A=(r\mathrm{sin}\theta\mathrm{d}\phi)(r\mathrm{d}\theta)=r^2(\mathrm{sin}\theta\mathrm{d}\theta\mathrm{d}\phi)$$

众所周知，立体角与球面面积的转换是

$$\Omega=\frac{A}{r^2}$$

因此

$$\mathrm{d}\omega=\frac{\mathrm{d}A}{r^2}=\mathrm{sin}\theta\mathrm{d}\theta\mathrm{d}\phi$$

带回去

$$\begin{align} \int_\Omega p(\omega)\mathrm{d}\omega&=1\\ \int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}c\mathrm{cos}\theta\mathrm{sin}\theta\mathrm{d}\theta\mathrm{d}\phi&=1\\ c\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\frac{1}{2}\mathrm{sin}2\theta\mathrm{d}\theta\mathrm{d}\phi&=1\\ \frac{1}{2}c\int_{0}^{2\pi}(-\mathrm{cos}2\theta\Big|_{0}^{\frac{\pi}{2}})\mathrm{d}\phi&=1\\ \frac{c}{2}\int_{0}^{2\pi}\mathrm{d}\phi&=1\\ c=\frac{1}{\pi} \end{align}$$

我们之前算过了雅可比矩阵，这里就直接用了，而且我们依然假设是单位球，半径为1，联合概率密度是

$$p(\theta,\phi)=\frac{\mathrm{cos}\theta\mathrm{sin}\theta}{\pi}$$

计算$\theta$边缘概率密度

$$\begin{align} p_\Theta(\theta)&=\int_{0}^{2\pi}\frac{\mathrm{cos}\theta\mathrm{sin}\theta}{\pi}\mathrm{d}\phi\\ &=\frac{\mathrm{cos}\theta\mathrm{sin}\theta}{\pi}2\pi\\ &=2\mathrm{sin}\theta\mathrm{cos}\theta\\ &=\mathrm{sin}2\theta \end{align}$$

计算$\theta$边缘概率密度的cdf

$$\begin{align} P_\Theta(\theta)&=\int_{-\infty}^{\theta}\mathrm{sin}2\theta\mathrm{d}\theta\\ &=\int_{0}^{\theta}\mathrm{sin}2\theta\mathrm{d}\theta\\ &=\int_{0}^{\theta}\frac{1}{2}\mathrm{sin}2\theta\mathrm{d}2\theta\\ &=\frac{1}{2}(-\mathrm{cos}2\theta\Big|_{0}^{\theta})\\ &=\frac{1}{2}(1-\mathrm{cos}2\theta)\\ &=\frac{1}{2}(1-(1-2\mathrm{sin}^{2}\theta))\\ &=\mathrm{sin}^{2}\theta \end{align}$$

它的反函数是

$$P_{\Theta}^{-1}(\theta)=\mathrm{sin}^{-1}(\sqrt{\xi})$$

计算相对于$\theta$来说，$\phi$的条件概率密度

$$\begin{align} p_\Phi(\phi)&=\frac{p(\theta,\phi)}{p_\Theta(\theta)}\\ &=\frac{1}{2\pi} \end{align}$$

和上面一致，直接写结果了

$$P_\Phi^{-1}(\phi)=2\pi\xi$$

概率分布转换

$$\left\{ \begin{align} \theta&=\mathrm{sin}^{-1}(\sqrt{\xi})\\ \phi&=2\pi\xi_{2} \end{align} \right.$$

又因为

$$\begin{align} \mathrm{sin}^{2}\theta+\mathrm{cos}^{2}\theta&=1\\ \xi_1+\mathrm{cos}^{2}\theta&=1\\ \mathrm{cos}\theta=\sqrt{1-\xi_1} \end{align}$$

带入直角坐标系转球面坐标系

$$\left\{ \begin{align} x&=\sqrt{\xi_1}\mathrm{cos}(2\pi\xi_2)\\ y&=\sqrt{\xi_1}\mathrm{sin}(2\pi\xi_2)\\ z&=\sqrt{1-\xi_1} \end{align} \right.$$